Artificial Neural Network - Effect of Adaptive Learning Rate
- May 14, 2017
- 5 min read
All codes related to this tutorial can be found at my Github repository.
For better understanding, before starting with this tutorial prefer to go through my previous tutorial on Artificial Neural Network
In previous implementation, We have kept learning rate constant throughout the training. We can apply a trick here also to make training faster.
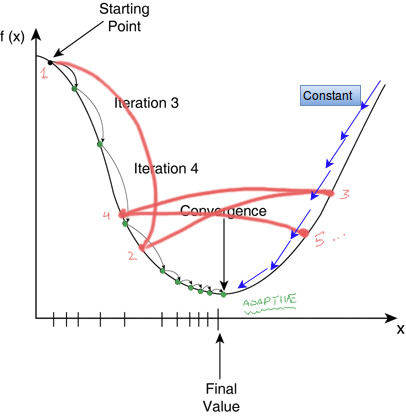
Figure 1. Learning rate and convergence
As illustrated in Figure 1, in any machine learning technique our goal is to minimize error and to achieve global Minima with function f(x). global Minima is the point in the n dimensional space where error is minimum and our predictions are very close to actual ones.
In given Figure 1. our goal is to reach convergence point and we have three choices
1) With constant learning rate reach to convergence, it wold take longer time [BLUE]
2) With larger learning rate try to reach to convergence and ultimately get diverted. with no convergence at all. [RED]
3) Middle approach between above two, initially keep high learning rate (bigger steps), and slowly decrease step size. [GREEN]
To accelerate the convergence and yet avoid the danger of instability, we can apply two heuristics:
Heuristic 1 - If the change of the sum of squared errors has the same algebraic sign for several consequent epochs, then the learning rate parameter, α, should be increased.
Heuristic 2 - If the algebraic sign of the change of the sum of squared errors alternates for several consequent epochs, then the learning rate parameter, α, should be decreased.
Here we are going to take help of our old friends squared error and trend-line function.

Figure 2. Change in Squared error w.r.t. Learning progress
In Figure 2. we have measured slops at different locations throughout the progress of learning (epochs). It is very much evident that when learning is faster the error will steeply decrease and value of slop will increase in consecutive steps (e.g. flop m2 is higher than m1) when decrease in error become slower the slop will decrease in consecutive steps (e.g m3 is smaller than m2). looking at increase and decrease in slop behavior we can change learning rate accordingly.
So the overall process can be summarized in two steps:
1) Increase the learning rate by certain percentage when slop at given point is greater than previous one.
2) Decrease the learning rate by certain percentage when slop at given point is lesser than previous one.
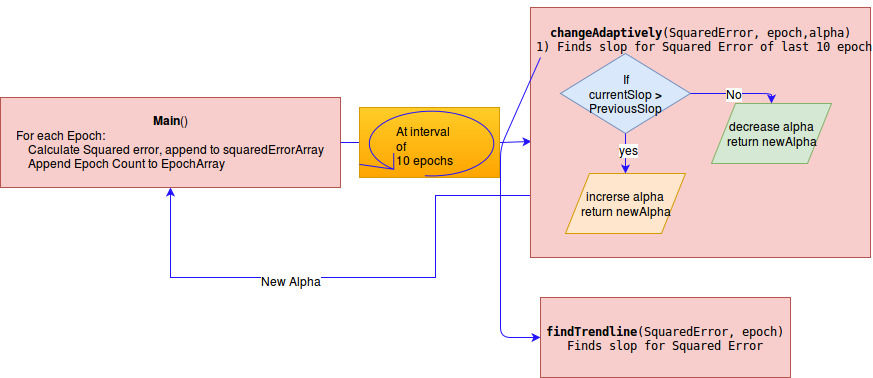
Figure 3. illustarting process of change in learning rate (alpha)
Along with our previous Artificial neural network code, we will be having two more functions
1) Initializing all network parameters
2) findTrendline - To find trend-line
3) changeAdaptively - To measure increase or decrease in slop w.r.t. previous point and accordingly change learning rate.
4) Main function - which is very similar to the simple Artificial Neural Network discussed previously.
1) Initializing all network parameters: defining XOR gate, initilalizing weights and bias. slopArray is declared as global as it would store slop for all epochs (iteration).
import math
"""
defining XOR gate, [x1, x2 , y]
"""
XOR = [[0, 1, 1], [1, 1, 0], [1, 0, 1], [0, 0, 0]]
# initialising weights
w13 = 0.5
w14 = 0.9
w23 = 0.4
w24 = 1.0
w35 = -1.2
w45 = 1.1
t3 = 0.8
t4 = -0.1
t5 = 0.3
# defining learning rate
alpha = 0.5
# initialising squaredError
squaredError = 0
# initializing error per case
error = 0
# defining epochs
Epochs = 2000
count = 0
# run this repeatedly for number of Epochs
global slopArray # to store slops
slopArray = []
2) To find trend-line we use following function
def findTrendline(xArray, yArray):
"""
used to find trend-line
:param xArray: Array with all elements in X
:param yArray: Array with all elements in Y
:return:
"""
# print xArray
# print yArray
xAvg = sum(xArray) / len(xArray)
yAvg = sum(yArray) / len(yArray)
upperPart = 0
lowerPart = 0
m = 0
# implementing mathematics behind trendline
for i in range(0, len(xArray)):
upperPart += (xArray[i] - xAvg) * (yArray[i] - yAvg)
lowerPart += math.pow(xArray[i] - xAvg, 2)
m = upperPart / lowerPart
b = yAvg - m * xAvg
return m, b
3) changeAdaptively - To make increase or decrease in learning rate after looking at current and previous slop.
def changeAdaptively(squaredErrorArray, EpochArray, alpha):
"""
to change learning rate(alpha) adaptively
:param squaredErrorArray: Array containing squared error for all completed epochs: [1.2340,0.1,0.45,0.85,0.4,0.4430,0.3244]
:param EpochArray: Array containing all completed epochs: [1,2,3,4,5,....50,51.]
:param alpha: [current learning rate]
:return:
"""
# print "went ti this func"
# print squaredErrorArray[-10:],EpochArray[-10:]
m, b = findTrendline(squaredErrorArray[-10:], EpochArray[-10:]) # find slop for current lat 10 error value
try:
if m > slopArray[-1]: #slopArray[-1] previous slop, m current slop
"""
If present slop is greater than previous one, it indicates decrease in error gradually
This usually happens at beginning and middle of learning process
then increase learning rate further to decelerate error further
"""
slopArray.append(m)
newAlpha = alpha * 1.08
else:
"""
If present slop is less than previous, it indicates instability or very less chane in error
this usually happens near to convergence point.
then decrease learning rate
"""
slopArray.append(m)
newAlpha = alpha / 1.04
return newAlpha
except:
# for first iteration when nothing will be there in slopArray
# so slop will throw exception and will be handled by except block
slopArray.append(m)
return alpha
4) Main function
def Main():
EpochArray = []
squaredErrorArray = []
for j in range(Epochs):
# printing squaredError, alpha after each epoch
print"squaredError", squaredError, alpha
# making update to learning rate after every 10 epochs
if j % 10 == 0 and j != 0:
alpha = changeAdaptively(squaredErrorArray, EpochArray, alpha)
# appending squared error to squaredErrorArray
squaredErrorArray.append(squaredError)
# appending number of completed epochs to EpochArray
EpochArray.append(j)
squaredError = 0
for i in range(4): # iterating through each case for given iteration
"""
calculating output at each perceptron
"""
y3 = 1 / (1 + math.exp(-((XOR[i][0] * w13) + (XOR[i][1] * w23 - t3))))
y4 = 1 / (1 + math.exp(-(XOR[i][0] * w14 + XOR[i][1] * w24 - t4)))
y5 = 1 / (1 + math.exp(-(y3 * w35 + y4 * w45 - t5)))
"""
calculating error
"""
error = XOR[i][2] - y5
"""
calculating partial error and change in weight for output and hidden perceptron
"""
del5 = y5 * (1 - y5) * error
dw35 = alpha * y3 * del5
dw45 = alpha * y4 * del5
dt5 = alpha * (-1) * del5
"""
calculating partial error and change in weight for input and hidden perceptron
"""
del3 = y3 * (1 - y3) * del5 * w35
del4 = y4 * (1 - y4) * del5 * w45
dw13 = alpha * XOR[i][0] * del3
dw23 = alpha * XOR[i][1] * del3
dt3 = alpha * (-1) * del3
dw14 = alpha * XOR[i][0] * del4
dw24 = alpha * XOR[i][1] * del4
dt4 = alpha * (-1) * del4
"""
calculating weight and bias update
"""
w13 = w13 + dw13
w14 = w14 + dw14
w23 = w23 + dw23
w24 = w24 + dw24
w35 = w35 + dw35
w45 = w45 + dw45
t3 = t3 + dt3
t4 = t4 + dt4
t5 = t5 + dt5
"""
Since y5 will be in float number between (0 - 1)
Here we have used 0.5 as threshold, if output is above 0.5 then class will be 1 else 0
"""
if y5 < 0.5:
class_ = 0
else:
class_ = 1
"""
uncomment below line to see predicted and actual output
"""
# print ("Predicted",class_," actual ",XOR[i][2])
"""
calculating squared error
"""
squaredError = squaredError + (error * error)
if squaredError < 0.001:
# if error is below 0.001, terminate training (premature termination)
break
After running code line no 6 in main function will print Squared error and alpha, this I have compared with the precious ANN code with constant alpha(0.5), After plotting three of them together I got following graph.
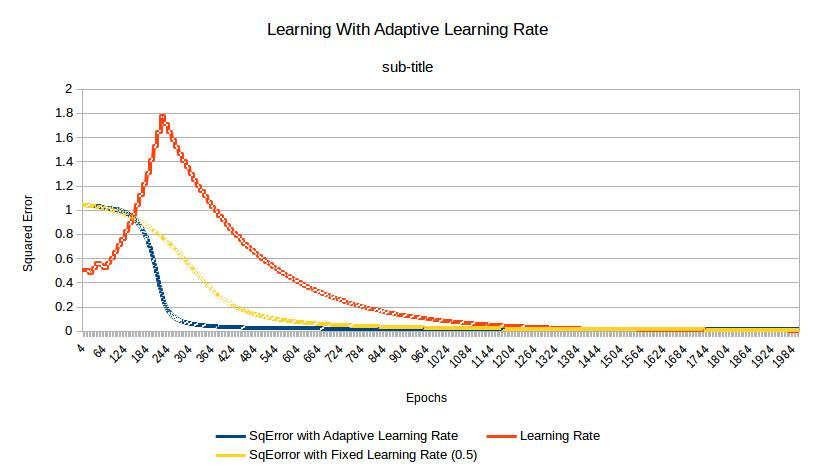
Figure. 4 Accelerated Learning with adaptive rate
In Figure 4, Initially learning rate remain very high up-to 350 epochs then it started decreases and also ensure faster convergence (blue line) w.r.t. the ordinary method without optimization (yellow line).






Comments